Column Buckling Equations

In the previous post in this series, we introduced some core concepts using a simplified idealised structure. In this post we’ll start to consider more realistic structures and determine the column buckling equations. In particular we’ll determine an expression for a critical load for an axially loaded column with pinned ends. Then we’ll explore some other support conditions.

We’ll cover quite a lot in this one, so here’s a table of contents…

Columns pinned at both ends
- Establishing the differential equation
- Solving the differential equation
- Solving for the constants of integration
Buckling modes and mode shapes
- Maximum deflection under critical load
- Higher order buckling modes
Columns with other support conditions
- Fixed-Fixed
- Fixed-Free
- Fixed-Pinned
Axis of buckling
Critical stress
Column effective length

When we refer to a pin support, this is a support that offers no resistance to rotation. Sometimes we come across pin supports in practice that very closely approximate this theoretical definition. Here are some examples:

Column Buckling Behaviour - Pinned supports

For the purposes of our discussion here, we’ll assume we’re dealing with pin supports like these, and that they don’t inhibit the rotation of the structure.

1.0 Buckling equation for columns pinned at both ends

In order to analyse this structure, we’re going to use the differential equation of the deflection curve in which $M$ is the internal bending moment at a given cross-section, $v$ represents the lateral deflection of the column and $x$ the distance along the length of the column. $EI$ is referred to as the flexural rigidity and is the product of Young’s modulus $(E)$ and the second moment of area of the cross-section $(I)$ .

EI\frac{\mathrm{d}^2v}{\mathrm{dx^2}}=M

💡This equation simply models the deflected shape of the column for a given flexural rigidity.

You’re likely to have come across this equation elsewhere in your engineering studies. Our laterally deflected column behaves in much the same way as a beam. Remember buckling is a bending failure rather than a failure due to direct compression (crushing). Our task now, is to use this equation to derive an expression for the critical axial load in a pinned-end column.

📌 Just as for the idealised structure discussed in the previous post, our derivation here will also assume all deflections are small by comparison to the size of the structure.

Establishing the differential equation

First consider the structure, its deflected shape and the free-body diagram that results from cutting the structure at a distance $x$ from the bottom support…

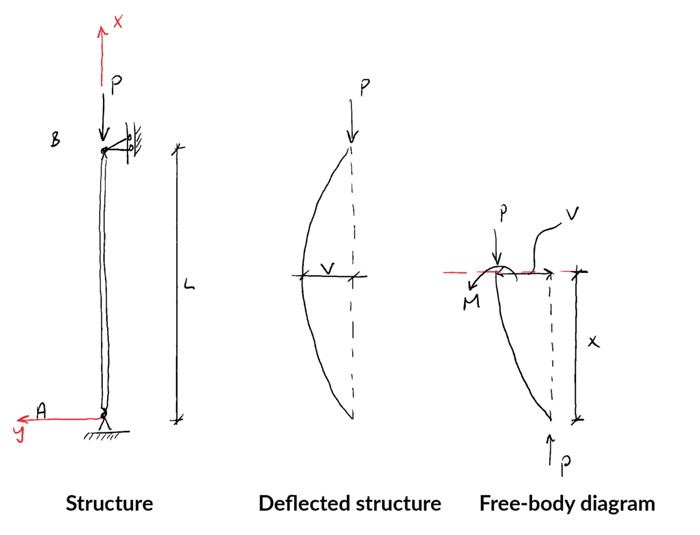
Taking moments about point A yields:

M=-Pv

Substituting $M$ back into the differential equation of the deflection curve and rearranging slightly yields:

\frac{\mathrm{d}^2v}{\mathrm{d}x^2} + \frac{P}{EI}v=0

This is a linear, homogeneous, 2nd order differential equation with constant coefficients. It also happens to be an equation that models the deflected shape of our structure and contains $P$ , the axial load. Following the same approach as for the idealised structure discussed previously, if we solve this equation we can determine $P_{cr}$ , the value of applied load at which it is balanced by the column’s flexural bending resistance.

So we’re faced with trying to solve a differential equation. At this point, it’s helpful to be able to point to the general solution of this form of differential equation:

v(x) = C_1 \sin\left(\sqrt{\frac{P}{EI}}x\right) + C_2\cos\left(\sqrt{\frac{P}{EI}}x\right)

Solving the differential equation

If you want to take a detour at this point to see how the differential equation is solved, watch the video below. Otherwise, we’ll continue working out the constants of integration in the next section.

Solving for the constants of integration

Now that we have the general solution for this format of equation, we need to solve for the constants of integration using the boundary conditions (pinned-pinned) for our column.

Boundary condition 1:

At $x=0$ (base of the column at pin support), $v=0$ (the lateral deflection must equal zero. Imposing these conditions on our general solution yields:

0=C_1\sin(0) + C_2\cos(0)

Therefore

C_2=0

As a result our solution reduces to:

v(x)=C_1\sin \left(\sqrt{\frac{P}{EI}}x\right)

Boundary condition 2:

At $x=L$ (top of the column at pin support), $v=0$ (lateral deflection also zero). Again, imposing these boundary conditions yields,

0=C_1\sin\left(\sqrt{\frac{P}{EI}}L\right)

So, either $C_1$ equals zero or $\sin(...)$ equals zero. If $C_1$ equals zero, the equation is satisfied for any value of $P$ . This doesn’t really move us forward…we can think of this solution as the trivial solution. Of more interest is the case where:

\sin\left(\sqrt{\frac{P}{EI}}L\right)=0

Knowing what we know about $\sin$ functions, this equation can only be true, when,

\sqrt{\frac{P}{EI}}L = 0, \pi, 2\pi,...n\pi

We can dismiss the case where,

\sqrt{\frac{P}{EI}}L = 0

In this scenario, $P$ would need to equal zero (as all other terms have non-zero values by definition) and we know this is not the case. So for a pinned-pinned column, our solution is:

\sqrt{\frac{P}{EI}}L = n\pi

where $n=1,2,3$ … Finally, we can rearrange this equation to make $P$ the subject of the equation:

P=\frac{n^2\pi^2EI}{L^2}

For $n=1,2,3,$ …

📌 This equation represents an infinite series of buckling loads. The lowest one $(n=1)$ is the critical buckling load, also known as the Euler Buckling Load $P_E$ .

P_E = \frac{\pi^2EI}{L^2}

2.0 Buckling modes and mode shapes

So far, we have established that there is an infinite series of buckling loads and the lowest one is the critical one and called the Euler Buckling load. This raises the question of what do the larger buckling loads correspond to?

These are loads that correspond to higher modes of buckling. Each mode of buckling has a corresponding buckled shape. To explore this further, refer back to our general solution after we established that $C_2=0$ :

v(x)=C_1\sin \left(\sqrt{\frac{P}{EI}}x\right)

Application of our second boundary condition resulted in us establishing the relationship:

\sqrt{\frac{P}{EI}}L = n\pi

Combining these two equations yields:

v(x)=C_1\sin\left(\frac{n\pi x}{L} \right)

for $n=1,2,3,$ … This equation describes the deflected shape of the column for each value of the buckling load $(n=1,2,3,...)$ defined above. Only when the axial load has one of the values given by the equation (previously defined)…

P=\frac{n^2\pi^2EI}{L^2}

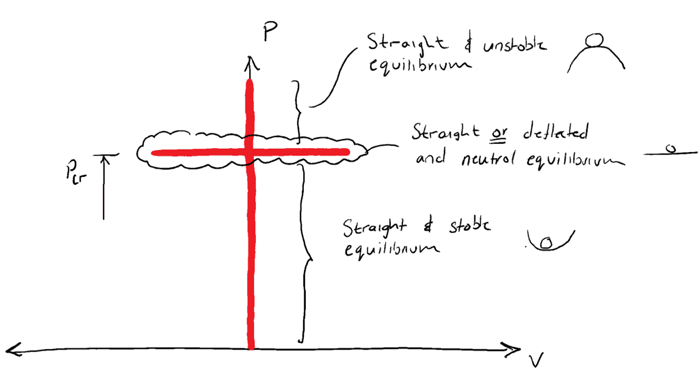
…can the column have a bent shape and be in equilibrium. For any other load, the column would be straight and in a state of STABLE equilibrium $(P< P_{cr})$ . We recall this concept from our previous discussion or idealised column structures in the last post:

Maximum deflection under critical load

Our equation for the deflected or buckled shape of a column contains the parameter $C_1$ , left over from our general solution to the differential equation. We now recognise that $C_1$ represents the magnitude of the sine wave or in this context, the maximum lateral deflection for the deflected/buckled deflection (defined above):

v(x)=C_1\sin\left(\frac{n\pi x}{L} \right)

If we now recall the states of equilibrium, when the column is in its buckled shape $(P=P_{cr})$ and in a state of neutral equilibrium, the maximum lateral deflection can have any value that still satisfies our small deflection assumption. We can represent the value of $C_1$ graphically…

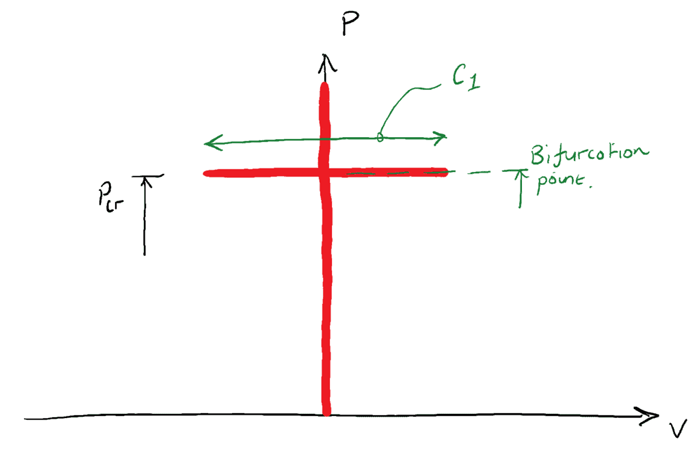
The value of $C_1$ is therefore mathematically undefined, it can have any ‘small’ value. Fortunately this doesn’t cause us any practical difficulty, as mentioned previously, the state of neutral equilibrium is not something we observe in civil engineering practice. For all intents and purposes, to a civil or structural engineer, a column experiencing $P_{cr}$ is considered to have failed. This theoretical state of neutral equilibrium is also known as a bifurcation point.

Higher order buckling modes

Imagine an axially loaded pinned end column that is restrained laterally at its mid-height point (by a floor slab say). The column would be prevented from buckling under the first critical (Euler buckling) load due to the lateral restraint. The floor slab restraint literally holds the column and stops it from buckling.

As a result of this restraint, the column can carry more load, until it reaches the second buckling load $(n=2)$ . As the column is not restrained against buckling in the second mode, it would now buckle (or theoretically enter into a state of neutral equilibrium).

💡Adequate lateral restraint increases a column’s resistance to buckling by ‘closing off‘ the possibility of buckling in lower modes and ‘unlocking’ higher buckling loads.

We can easily visualise the first three modes of buckling simply by evaluating the load and deflected shape equations for $n=1,2,3$ .

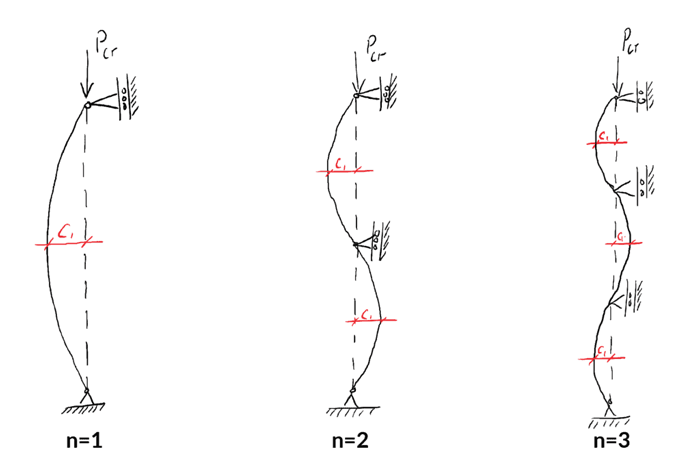
Mode

n=1

n=2

n=3

Critical Load

P_{cr} = \frac{\pi^2EI}{L^2}

P_{cr} = \frac{4\pi^2EI}{L^2}

P_{cr} = \frac{9\pi^2EI}{L^2}

Buckled Shape

v(x) = C_1\sin\left(\frac{\pi x}{L}\right)

v(x) = C_1\sin\left(\frac{2\pi x}{L}\right)

v(x) = C_1\sin\left(\frac{3\pi x}{L}\right)

📌 For any given mode, $P_{cr}$ represents the practical upper limit on axial load. Natural imperfections, for example column ‘out of plumb’ or poor load alignment will almost certainly induce buckling when the critical load is exceeded.

3.0 Columns with other support conditions

So far we’ve looked at the behaviour of a column pinned at both end. This is the typical starting point. But the same process can be followed to determine the corresponding equations for columns with different types of support conditions. In the videos below, I’ll carry out the derivations to demonstrate the process for:

Columns with a base fixed against rotation and free at the top (fixed-free)
Columns fixed against rotation at both ends (fixed-fixed)
Columns fixed against rotation at the base and pinned at the top (fixed-pinned)

Buckling equation for columns restrained against rotation at both ends (fixed-fixed)

Buckling equation for columns restrained against rotation at the bottom and free at the top (fixed-free)

Buckling equation for columns restrained against rotation at the bottom and pinned at the top (fixed-pinned)

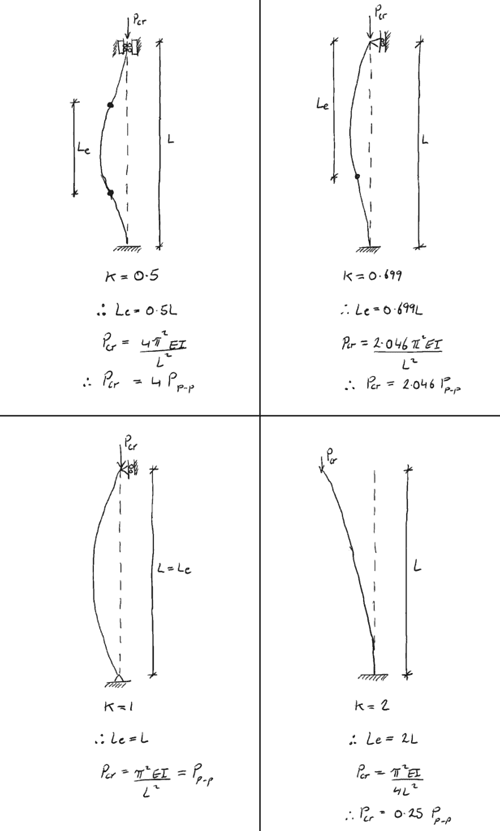
Support condition summary

4.0 Axis of Buckling

We recall from the equation for the buckling load that it is a function of I, the second moment of area of the cross-section:

P=\frac{n^2\pi^2EI}{L^2}

So for a given cross-section, a column will always buckle about the axis with the lower second moment of area, the ‘weaker’ axis. This assumes that both axes have equal restraint. Consider the case of a universal column (UC) section under compression:

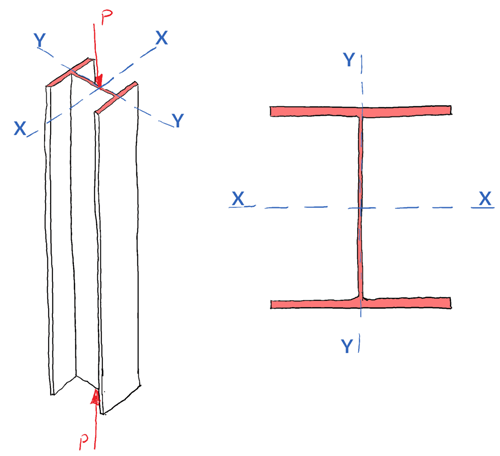
Since the X-X axis, is the major principal axis (with the largest value of second moment of area – you might remember this from your study of Mohr’s circle), it is the stronger axis and so the column will buckle about the minor principal or Y-Y axis first.

When considering the buckling load for a column structure, the cross-section shape plays a key role, you should evaluate the major and minor principal axes to determine the critical axis for buckling.

5.0 Critical Stress

📌 The critical stress is the average axial stress in a cross-section under the critical load

\sigma_{cr}=\frac{P_{cr}}{A}=\frac{\pi^2EI}{AL^2}

We now define the Radius of Gyration, as:

r=\sqrt{\frac{I}{A}}

We can therefore write the critical stress as:

\sigma_{cr}=\frac{\pi^2E}{\left(\frac{L}{r}\right)^2}

Finally we define the Slenderness Ratio as:

\lambda=\frac{L}{r}

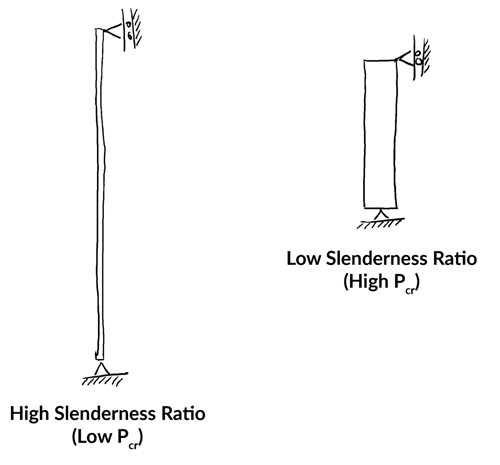
The slenderness ratio is a very useful measure of a column’s geometry and susceptibility to buckling. A high slenderness ratio indicates greater susceptibility to buckling. The slenderness ratio should be determined separately for each principal axis. We can get an intuition for the slenderness ratio by visualising both extremes,

The equation for critical stress can therefore be written as a function of the slenderness ratio as follows,

\sigma_{cr}=\frac{\pi^2E}{\lambda^2}

Plotting the critical stress versus slenderness ratio for a given value of Young’s modulus yields an Euler Curve showing the safe range of average axial stress for a given slenderness ratio (or the safe range of slenderness ratio values for a given axial stress),

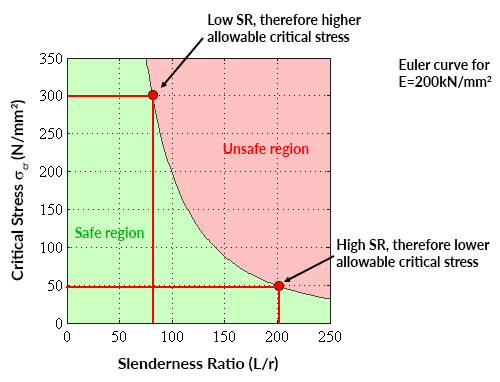
📌 An Euler curve is only valid for critical stresses below the material yield stress

6.0 Column Effective Length

The final concept we will look at in this post is column effective length. The effective length of a column, $L_e$ , is the length between points of inflection on the deflected curve/shape (even if the shape must be extended until a point of inflection is reached – discussed below). For a column pinned at both ends, the effective length is simply the full length of the column between pin restraints:

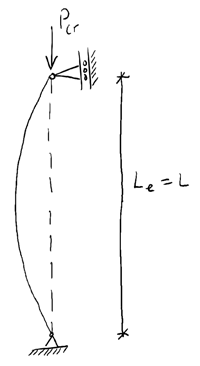
Consider a column with a fixed support at its base and no lateral restraint at the top (fixed-free). At the base, no rotation can occur. In order to obtain two inflection points on the deflected shape, it must be extended…

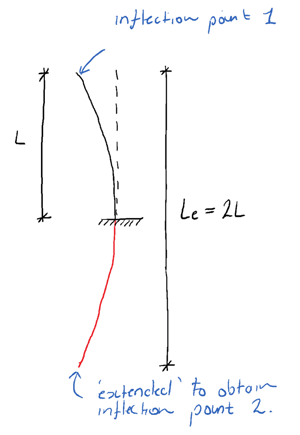
The ‘imaginary’ red portion of the deflected shape is the extension required to provide inflection point number 2. Thus the effective length for a fixed-free column is 2L.

📌 Another way to think about effective length is that it’s the length of an equivalent pinned end column.

Before concluding our discussion of effective length, we can define a general expression for the critical load as:

P_{cr}=\frac{\pi^2EI}{{L_e}^2}

If we now introduce the Effective Length Factor, $K$ , such that $L_e=Kl$ , we can state the critical load as a function of the effective length factor: