Reinforced Concrete Fundamentals - Analysis and Design of Steel Reinforcement
![[object Object]](/_next/image?url=%2Fimages%2Fauthors%2Fsean_carroll.png&w=256&q=75)
In the previous concrete tutorial, we introduced concrete – plain unreinforced concrete. In this tutorial, we’ll see that to take full advantage of concrete as a construction material, we need to combine it with steel reinforcement. This leads us nicely into the exciting world of reinforced concrete design. We take our first steps towards exploring this vast field in this tutorial.

Fig 1. (a) Steel reinforcement cages for columns, (b) Steel reinforcement cages for beams.
This tutorial is taken from lecture 13 and lecture 14 in my course, Fundamentals of Reinforced Concrete Design to Eurocode 2. After reading this, if you want to dive in further and understand how we design reinforced concrete for bending and shear, take a look at the course details below.
Fundamentals of Reinforced Concrete Design to Eurocode 2
An introduction to ultimate limit state design for bending and shear with optional calculation automation using Python.
After completing this course...
- You will be able to determine design actions using the Eurocodes Basis of Structural Design (EC0) and Actions on Structures (EC1).
- You will understand balanced section design and how to analyse and safely design singly and doubly reinforced concrete sections.
- You will understand how to apply the Variable Strut Inclination Method for shear reinforcement design.
- You will have developed your own reinforced concrete design codes in Python (the Python pathway is optional in this course).
1.0 Reinforced Concrete Design and Behaviour under Load
Checkout the video and lecture notes in the course..
Plain concrete on its own actually has quite limited value as a construction material. This is because concrete is brittle and has a relatively low tensile capacity by comparison to its compression capacity. A typical concrete with a compressive strength of would experience cracking under tensile loading at a stress of approximately .
For this reason, we introduce steel reinforcement as a means of resisting the tensile forces that develop in the concrete cross-section. Including steel reinforcement also leads to ductile failures, which are safer than sudden explosive brittle failures.
1.1 Steel Reinforcement
In a reinforced concrete structure, reinforcing steel or ‘rebar’ cages are used to provide the tension capacity required to balance the compression forces that develop in the concrete. We’ll explore this in much greater detail below. When resisting flexure, the compression forces in the concrete and tension forces in the rebar form a couple that resists the moment generated by applied loading.
Rebar in common use throughout Europe and the UK is high-strength steel with a characteristic yield strength of . Although they are notionally circular in cross-section they have a deformed surface to improve the mechanical bond between the steel and encasing concrete. They are supplied in common diameters; .
Individual bars are bent into shape and tied together to form reinforcement cages. Even today, this is still a manual, labour-intensive task. This, combined with the curing time needed for concrete leads to longer construction times compared to a similar structure constructed from structural steel for example. However, as we saw in the previous tutorial, concrete structures offer many other advantages to compensate for slower construction times.

Fig 2. Deformed high-strength steel reinforcement bars.
2.0 Reinforced concrete cross-section analysis
At this point, we’ve developed a good overall understanding of concrete’s strengths and weaknesses and a general understanding that embedded steel reinforcement compensates for concrete’s inherent weakness in tension. Next, we need to start exploring exactly how the steel and concrete act compositely to resist externally applied loading.
2.1 Stress-resultants and the internal moment of resistance
We’ll start by considering a simply supported beam subject to a uniformly distributed load (UDL). We can think of this loading as generating an external bending moment, .
In response, the beam generates a resistance to through the development of internal normal stresses in the material. These normal stresses can be represented by stress resultant forces (simply stress multiplied by the area over which it develops); one in tension, and one in compression, . The internal stress resultants, separated by a lever arm, , form a couple, . It is this internal couple or bending moment that resists the externally applied bending moment, Fig. 3. So far, this is classical beam bending theory – nothing specific to reinforced concrete behaviour.
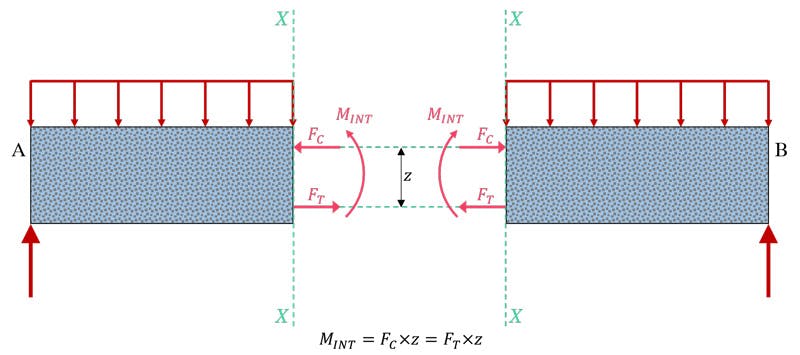
Fig 3. Simply supported beam, with a cut at section , revealing the internal stress resultants, and and corresponding internal bending moment, which resists the externally applied loading.
As mentioned earlier, concrete is strong in compression but comparatively weak in tension, with a tensile capacity of approximately of its compression capacity. Therefore we must use reinforcing steel to provide tensile resistance. In fact, when considering the ultimate moment capacity of a concrete beam, we conservatively assume the concrete has no tensile capacity whatsoever and that the section is cracked between the extreme tensile fibre and the neutral axis.
2.2 Stress and strain distributions in reinforced concrete
Consider again the simply supported reinforced concrete beam subject to a UDL. The external loading will induce stresses internally within the beam. When we make an imaginary cut (shown above in Fig 3), we expose the internal stresses acting on the exposed cross-section. The cross-section we are referring to is shown in Fig. 4.
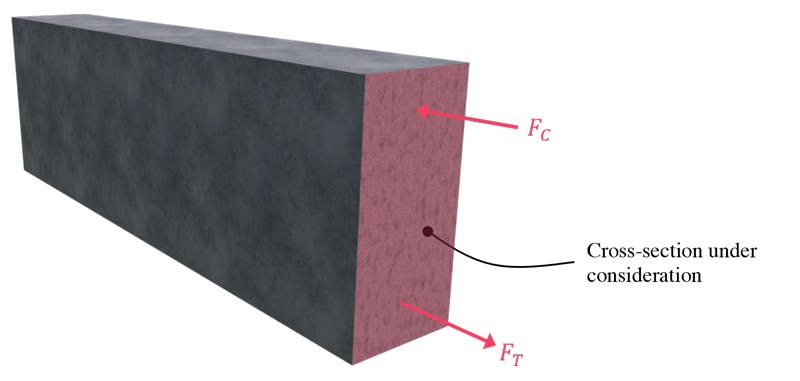
Fig 4. The red shaded area is the section under consideration in the following discussion on section analysis.
Before proceeding any further, we also define the ultimate moment of resistance of a reinforced concrete section as the maximum value of the internal moment that can be generated, beyond which either the concrete would fail in compression or the steel would yield in tension.
Now, consider the cross-section identified in figures 3 and 4. The orientation of the loading is such that the top fibres of the beam will be in compression and the bottom fibres in tension. In Fig. 5 (a) below, we can see an elevation view of the section and its associated dimensions and in (b), we can see how the strain varies with height across the section.
Figures (c), (d) and (e) represent three possible stress distribution diagrams:
- Figure (c) shows a linear stress distribution. As we saw in the previous tutorial, stress is not linearly proportional to strain in plain concrete. However, for relatively low levels of strain, we can reasonably approximate stress as being linearly proportional to strain. This assumption is synonymous with serviceability limit state analysis.
- Figure (d) is referred to as the rectangular-parabolic stress block and is observed at the point of concrete compression failure. The stresses at the outermost (furthest from the neural axis) fibres have reached their compression limit .
- Figure (e) represents the equivalent rectangular stress block. This stress block is an approximation of the rectangular-parabolic stress block. It yields almost identical numerical results while being much easier to manage numerically.
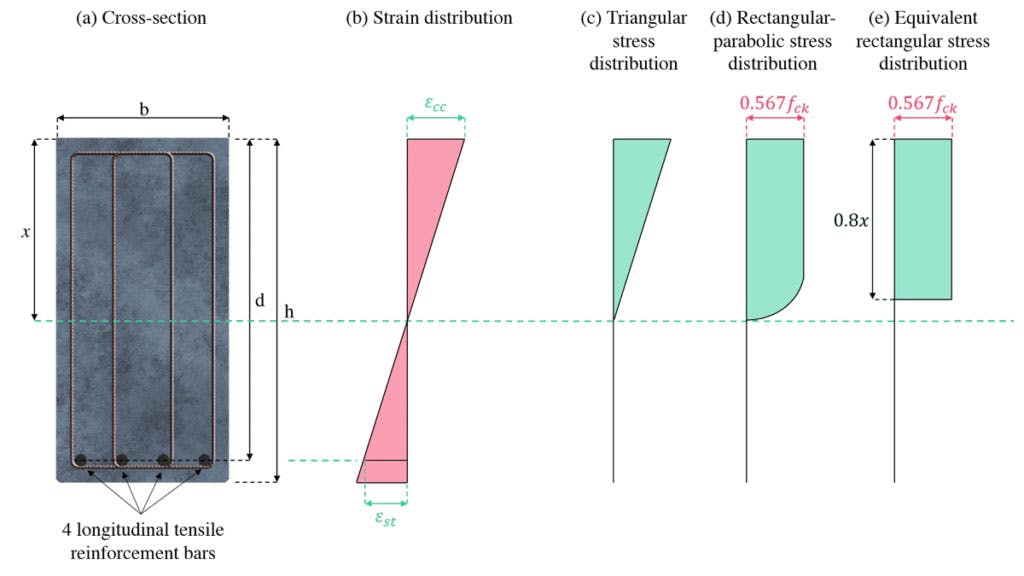
Fig 5. (a) Concrete cross-section, (b) strain distribution and (c-e) three possible stress distributions.
In all three stress diagrams, the tensile stress is only developed at the level of the reinforcing steel, i.e. tensile stresses are only developed in the steel. The concrete in all cases is assumed to be cracked up to the height of the neutral axis and therefore does not provide any tensile resistance. This is a fundamental assumption of ultimate limit state (ULS) section analysis.
2.3 Balanced section design
Now we can start to think about the limits imposed by fundamental material behaviour. Remember, our models of material behaviour dictate that the steel will yield at a strain value of , while the concrete will crush at a compressive strain . Looking at the strain distribution in Fig. 5(b), using basic geometry (similar triangles), these two strain limits can be used to determine the position of the neutral axis as a function of the effective depth, (distance from the top of the compression zone to the centre of the steel reinforcement):
If the neural axis is in this position when the beam is subject to its ultimate load, in theory, the concrete will crush in compression, and the steel will yield in tension simultaneously. This is referred to as a balanced section design.
This is not a desirable mode of failure. Concrete compression failures are brittle failures providing little or no visible warning signs, whereas yielding of steel is a ductile failure. A ductile beam failure, one in which the steel yields before the concrete crushes, is preceded by a period of pronounced tensile cracking of the concrete. This provides a warning that a failure is possible, even likely.
For this reason, we design concrete sections to fail due to yielding of the steel first. Practically we do this by placing limits on the position of the neutral axis, and we do this by controlling how much reinforcing steel we place in the cross-section. Put simply, if we put too much steel in our beam, the tensile force that can be developed in the steel reinforcement will be larger than the compressive force that the concrete can resist, so the concrete will fail first – a sudden, explosive, brittle failure.
The material properties and geometry of the section dictate that for a ductile failure (steel yielding first), the neutral axis, . However, the Eurocode specifies that . This means that when the steel has yielded, the concrete strain is far enough away from its ultimate value to allow further rotation of the section to occur.
To further emphasise the meaning of this limit on neutral axis depth, consider the strain distribution in Fig. 6. If we impose the condition that at the instant of failure, the steel will have yielded, the bottom strain value is fixed at .
Now, if the neutral axis was permitted to be as low as , this would result in the strain in the concrete being equal to the ultimate value of , or a balanced design, as discussed above. However, if we limit the neutral axis depth to , the maximum strain in the concrete will be the value shown, . This leaves an additional capacity strain of .
This allows rotation of the beam to continue after the steel has yielded but before the concrete crushes in compression. This further rotation is referred to as plastic rotation or plastic hinge behaviour and allows redistribution of moments to take place in the structure, provided it has sufficient structural redundancy.
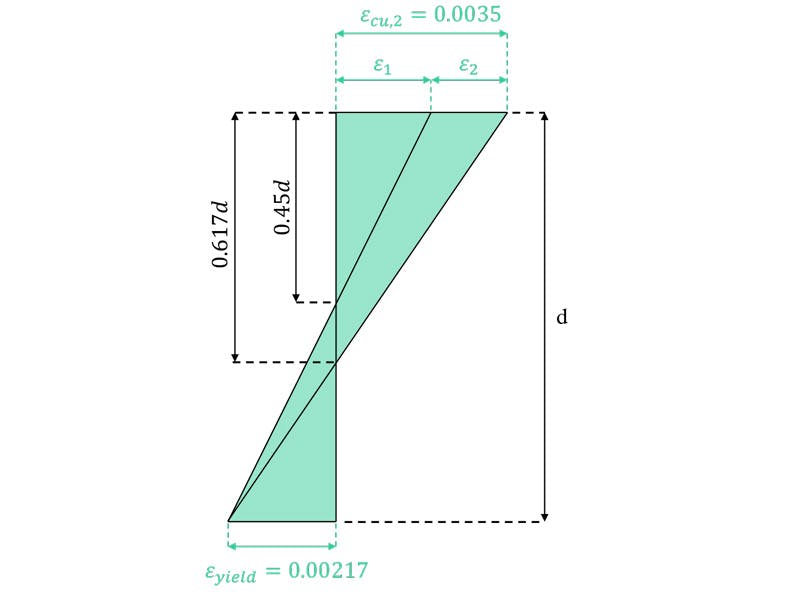
Fig 6. Limits on neutral axis depth.
3.0 Ultimate Moment Capacity of Reinforced Concrete
Checkout the video and lecture notes in the course..
Now that we’ve introduced the concept of balanced section design and understand the limit placed on neutral axis depth, our next task is to develop a set of design equation that respect this limit. We’ll focus here on so-called singly reinforced concrete sections, taken from a typical beam.
The term ‘singly reinforced’ refers to the fact that reinforcing steel is provided in the tension zone of the beam. Later in your study of reinforced concrete, you’ll see that we can also reinforce the compression zone, such sections are referred to as doubly reinforced and are covered further in Fundamentals of Reinforced Concrete Design to Eurocode 2.
3.1 Ultimate moment of resistance – singly reinforced concrete section
Let’s start by considering the reinforced concrete beam cross-section shown in Fig. 7 below.
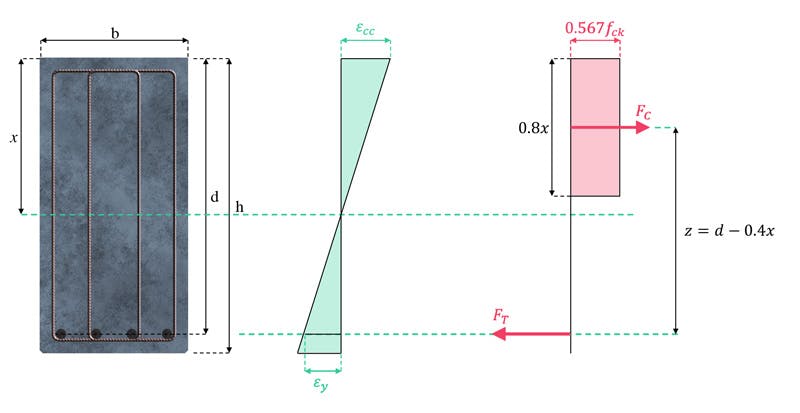
Fig 7. Reinforced concrete section showing stress and strain distribution at the ultimate limit state.
The beam from which the cross-section was obtained is subject to a bending moment that induces compression on the top of the section. The beam is reinforced with steel in the tension zone only.
The strain and stress distribution at failure are also shown. The task now is to determine an expression for the ultimate moment capacity of this section that ensures a ductile failure, i.e. where the steel yields in tension before the concrete crushes in compression.
Let’s state at the outset that the internal bending moment is equal in magnitude to the externally applied bending moment, thus . To be consistent with Eurocode nomenclature, we will refer to external bending moments as design moments (as in, moments we are designing for), denoted by (where the subscript stands for the effect of actions). An internal bending moment shall be referred to as a moment of resistance, denoted by . Therefore, at risk of stating the obvious, we seek to achieve .
where and are the compression and tension stress resultants acting on the cross-section and is the lever-arm between them.
The compressive stress resultant (in the concrete), is simply the stress magnitude multiplied by the area over which it acts,
Noting that the lever-arm is , we can obtain an expression for the internal moment of resistance as a function of the neutral axis depth ,
Remembering that at the point of failure, the neutral axis is limited to a depth of , we can substitute this into the Eqn. 4, the expression then simplifies to:
This equation can be interpreted as:
where . This is the maximum bending moment that can be generated in a singly reinforced beam while still respecting the neutral axis depth limit, ensuring a ductile failure.
3.2 Area of steel reinforcement
So far, we’ve established the ultimate moment our beam can safely resist. Notice that this simply required that we state the characteristic cylinder strength and cross-section dimensions. However, we still need to determine how much steel reinforcement is required to generate this moment of resistance.
Remember, if we don’t put enough steel into the beam, the steel we do provide will yield too soon, i.e. before the ultimate moment capacity can be generated. If, on the other hand, we put too much steel in, the beam will continue to resist loading until the concrete crushes in compression; this would give a higher moment capacity but a brittle (unsafe) failure. So we need to identify the specific area of steel required.
Consider again the section in Fig. 7 and Eqn. 4 above. If we replace the lever-arm with and instead of stating the height of the stress block as , we use the equivalent expression, , we can write an equivalent expression for in terms of the lever arm , rather than ,
Now, letting and imposing the limit that , rearranging we get a quadratic equation in ,
Solving this quadratic for , we obtain:
Using Eqn. 8, we can obtain an expression for the lever arm, , based on the externally applied design moment, geometry of the beam and its material properties. The required area of steel can now be simply determined by considering the steel stress at failure:
since
we have:
So in summary, the key equations when designing a singly reinforced beam for a ductile failure are:
4.0 Wrapping up and where to next?
In this tutorial, we’ve introduced the role of steel reinforcement in reinforced concrete design. We’ve seen that steel plays a critical role in the development of an internal moment of resistance and compensates for the concrete’s inherent brittleness and weakness in tension.
We’ve also explored the fundamental mechanical model used to describe the behaviour of the cross-section under load. We’ve seen that to avoid a brittle failure, we must limit the depth of the neutral axis at the ultimate limit state.
Although we’ve covered a lot of ground and established a strong foundational understanding of reinforced concrete, we’ve really only scratched the surface. There are numerous other cross-section configurations to explore, not to mention how resistance to shear force is developed.
If you want to explore reinforced concrete design further, take a look at the course below. After completing that course, you’ll have a much more complete understanding of fundamental reinforced concrete behaviour.
That’s all for now. I’ll see you in the next one.
Fundamentals of Reinforced Concrete Design to Eurocode 2
An introduction to ultimate limit state design for bending and shear with optional calculation automation using Python.
After completing this course...
- You will be able to determine design actions using the Eurocodes Basis of Structural Design (EC0) and Actions on Structures (EC1).
- You will understand balanced section design and how to analyse and safely design singly and doubly reinforced concrete sections.
- You will understand how to apply the Variable Strut Inclination Method for shear reinforcement design.
- You will have developed your own reinforced concrete design codes in Python (the Python pathway is optional in this course).
Dr Seán Carroll's latest courses.

Featured Tutorials and Guides
If you found this tutorial helpful, you might enjoy some of these other tutorials.
Understanding Tresca and von Mises Elastic Failure Theories
Go from the fundamentals of elastic failure theory to implementing section analysis in Python using sectionproperties

Julian Haudek
Parametric Graphic Statics with GeoGebra
Increase the precision and speed of your analyses with parametric graphic statics.

Prof Edmond Saliklis




