Column Buckling and Stability

Long slender structural elements under the action of an axial load may fail due to buckling rather than direct compression. Buckling failure occurs when axial load induces a lateral deflection leading to a bending type failure. Buckling can also occur in plate and shell structures and is a relatively common cause of structural collapse. Depending on the geometry of the structural element, buckling can occur long before the material yields.

💡Columns rarely fail in direct compression, buckling usually occurs first

The Idealised Structure

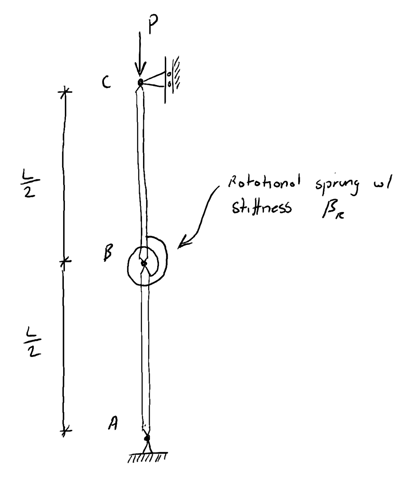
As a starting point to understanding buckling behaviour – let’s consider an idealised (simplified) structure that we can use as the basis for mathematical modelling. Our structure consists of 2 rigid bars connected by a rotational spring…

Note the following about the structure:

• The rotational spring has a stiffness of $\beta_R$

• Both bars are perfectly aligned and the external load $P$ is applied directly through the longitudinal axis

• Under ideal conditions the system is in compression and the spring in not under any load

Adding a small lateral displacement

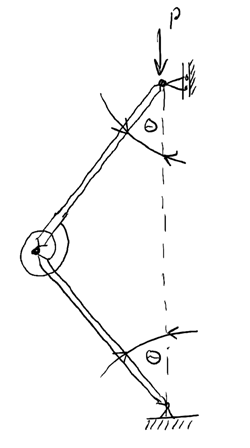
Think about what happens if we impose a small lateral displacement on the structure…

The rotational spring applies a restoring moment $M_B$, equal to the angle through which the spring rotates multiplied by the spring’s rotational stiffness:

The restoring moment acts to decrease the lateral displacement while the axial load, $P$, tries to increase it.

At this point, two things could happen:

• If the axial load is ‘small’,  $M_B$ wins and the structure straightens up returning to its original position/state

💡The structure is said to be STABLE

• If the axial load is ‘large’, P wins, and the lateral displacement continues until the structure collapses

💡The structure is said to be UNSTABLE

At some point we must cross a boundary between the stable and unstable states. This boundary is characterised by the critical load $P_{cr}$.

Much of the discussion that follows will now focus on determining what the critical load is for a variety of column end conditions.

Determining the critical load for the idealised structure

To determine the critical load for our idealised structure, we can ‘cut’ the structure at the location of the spring and consider equilibrium of the top half, the resulting free body diagram reveals the moment action of the spring at the cut end of the structure…

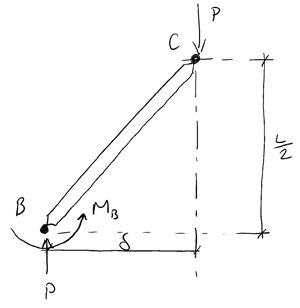
• Note that we have vertical force equilibrium as a result of the internal axial force revealed by the cut at B
• We also have moment equilibrium due to the couple creating by both P forces balancing $M_B$.
• If we assume that the displacement of the system is small, we can approximate the lateral deflection as:

So, taking the sum of the moments about B and assuming clockwise moments are positive yields:

Now since we know, $\theta$ isn’t equal to zero, the expression in brackets must equal zero. So solving for $P$ yields:

This is the value of $P$ for which the external axial load is balanced by the restoring moment of the rotational spring, as such, from what we said above, this is the critical load for our idealised structure, i.e. the axial load at which it is on the boundary between being stable and unstable.

Equilibrium and Stability

It’s important to establish a clear understanding of what we mean when using the terms equilibrium and stability, particularly in the context of a discussion on buckling.

When $P$

The idealised structure is straight and in equilibrium.

If a small lateral deflection is imposed on the structure, it will return to the straight position. A good analogy for this is a ball sitting on a concave surface. The ball will always return to the same stable state of equilibrium when not disturbed.

When $P>P_{cr}$

The idealised structure is straight and in a state of equilibrium

The structure is in a precarious (unstable) state of equilibrium. The smallest possible lateral deflection or disturbance will cause the structure to buckle. From an engineering perspective we must avoid this state.

The corresponding ball analogy is that of a ball precariously positioned at the top of a convex surface…the smallest disturbance will set the ball rolling.

When $P=P_{cr}$

💡What happens if P=$P_{cr}$? and we apply a small lateral deflection??

In this case the disturbing effect of the axial load is matched by the restoring effect of the moment $M_B$.

This case is analogous to a ball sitting on a perfectly flat surface. We can visualise the various states of equilibrium in a graph of axial load versus angle of rotation…

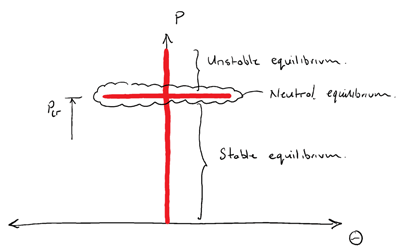
• All points identified in red, represent states of equilibrium
• Notice that ‘in theory‘, for an undefined range of $\theta$ (angles of rotation), when $P=P_{cr}$, we have a state of neutral equilibrium and the structure could keep deflecting.

From a practical point of view, we always aim to maintain axial loads well below the critical buckling load for a structure. The concept of neutral equilibrium can be thought of as a theoretical state that is highly unlikely to be observed in practice.

Up to this point we’ve discussed a simplified idealised structure that has all of its resistance to rotation concentrated at the midpoint in a rotational spring. This has allowed us to get a feel for some important concepts.

In the next post, we’ll expand to start thinking about more realistic structures that have distributed flexural rigidity.