How to Apply the Virtual Work Method to Trusses
![[object Object]](/_next/image?url=%2Fimages%2Fauthors%2Fsean_carroll.png&w=256&q=75)
In this tutorial, you’ll see how we can use the virtual work method to analyse trusses and calculate truss deflections. The virtual work method is based upon the Principle of Virtual Work, which we’ll explore further below.
The Principle of Virtual Work underpins many elegant and versatile analysis procedures. We’ll focus here on how it can be applied to trusses, but we can equally use it to analyse beam and frame structures.
This tutorial will initially develop the underlying theory, starting with the concept of strain energy. This will make the jump to virtual work much easier to understand. We’ll bring it all together with a thorough worked example at the end.
1.0 Strain energy and the virtual work method
The virtual work method is an energy-based analysis method. The key to understanding how and why it works is to first understand the concept of strain energy and how it applies to axially loaded structural elements. When we understand strain energy, we can more easily expand to the broader Principle of Virtual Work and the associated analysis methods.
Let’s start by considering a simple bar, with original length , in uniaxial tension under the action of a force . Under the influence of this force, the bar will get longer as a result of the tensile strains that develop. So, let’s say the bar extends by a distance , Fig 1.
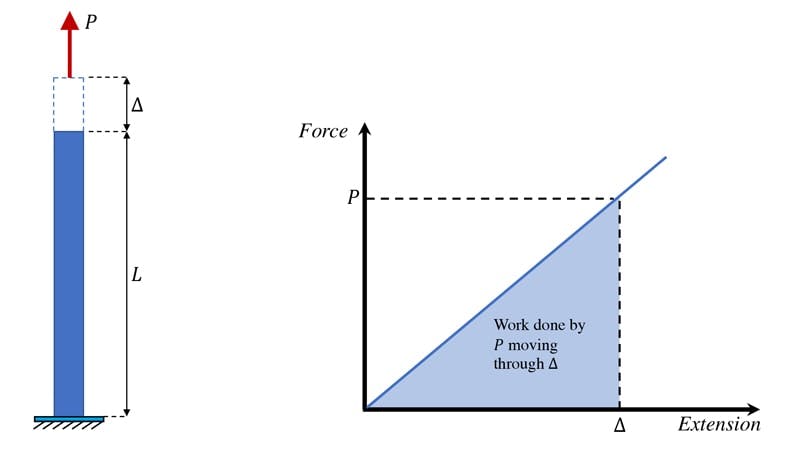
Fig 1. Bar in uniaxial tension (left) and axial load versus deflection graph (right).
This means that the force has moved through a distance and as such, the force does work on the bar. If we assume the bar is linearly elastic, then the work done by the force, on the bar, is obtained as the area beneath the load-deflection graph.
Based on the principle of conservation of energy, we know that energy cannot be created or destroyed, it can only be transformed from one form to another. So, the work done by the force is transferred into stored potential energy in the bar. In other words, the internal state of stress in the bar, as a result of being compressed, results in a store of potential energy in the bar.
This is analogous to the stored energy in a spring after it has been compressed, the more work the external force does in compressing the spring, the more stored potential energy the spring has. We can summarise this energy relationship by simply stating;
where and represent work and strain energy respectively. So, we can say therefore that strain energy is given by,
Since the bar is linearly elastic, we know that stress in linearly proportional to strain with Young’e modulus, , as the constant of proportionality, therefore,
where is the cross-sectional area of the bar. Rearranging, we obtain an expression for ,
If we now substitute this expression for into our original expression for strain energy, we obtain,
Now we can state the conservation of energy principle as it applies to the bar, mathematically,
where we are now distinguishing between the externally applied force, and the internal axial force, . Of course these are numerically equal but we make the distinction for clarity.
This energy equation is equally applicable for the work done on a collection of axially loaded elements – which you and I know as a truss! So if we expand to consider a force applied to a truss consisting of members, we have,
where is the distance through which the externally applied force moves. Using this equation we can easily evaluate the deflection , provided we can determine all of the forces in the structure using something like the method of sections or joint resolution method.
This is a good starting point and clearly demonstrates the underlying principle of conservation of energy. But the strain energy equation is somewhat limited in its application since the only displacement we can directly evaluate is the displacement along the line of action of the externally applied force. This is where the broader Principle of Virtual Work and Virtual Work Method come in.
2.0 The Principle of Virtual Work
The Principle of Virtual Work is also based on conservation of energy. It states that when an equilibrium force system is moved by a small compatible displacement system, the work done by the applied loads is equal to the change in strain energy in the structure.
We can immediately recognise the similarity with our previous discussion of strain energy. What’s new is the introduction of two specific terms:
- Equilibrium force system: this is simply a system of forces in equilibrium and encompasses both internal and external forces.
- Compatible displacement system: this is a system of displacements the structure could experience.
Together the equilibrium force system and the compatible displacement system are the building blocks of the virtual work method and are what make the analysis technique more versatile than the simple strain energy analysis we developed in the previous section.
The versatility of the virtual work method comes from the fact that we can combine any equilibrium force system with any other compatible displacement system. This means that the compatible displacement system does not necessarily need to be the system of displacements that correspond to the applied external loads.
In this way, we can decouple the compatible displacement system and equilibrium force system. This means that we can select whatever compatible displacement system or equilibrium force system we like, depending on what we’re trying to solve for.
2.1 The Virtual in Virtual Work
One thing that often throws people when first learning about virtual work is the presence of the work virtual! It’s an unusual word in this context and tends to make things sound more complicated then they really are – so let’s see where it comes from.
Let’s say we want to determine the deflection at some point in our truss. In this case we would construct our analysis in the following way; we would let the real (unknown) displacement be the compatible displacement system.
To use the virtual work method, we also need an equilibrium force system. Remember, this can be any system of forces in equilibrium. So, let’s apply a load to the structure. The location and direction of this load will depend on what displacement we’re trying to find.
This external force and the internal forces it induces in the structure now serve as our equilibrium force system. With both systems established, we can apply the principle of virtual work (we’ll get to this below) and solve for the unknown displacement.
Since the force wasn’t actually applied to the structure in reality – we say it’s a virtual force. And since the force was virtual the work done by the force was also virtual, hence the virtual work method, it’s as simple as that! In this scenario, where the displacement is unknown, we end up with a real compatible displacement system and a virtual equilibrium force system.
Now let’s imagine the less common case where we want to use the virtual work method to identify an unknown force. In this scenario, we let the real unknown forces by the equilibrium force system and apply a virtual displacement to form the compatible displacement system.
When we apply the virtual work method, our unknown force will emerge from the analysis. Just as before, the work done by the equilibrium force system as it moved through the compatible displacement system is still virtual.
Before we move on to the details of the analysis procedure itself, we’ll clarify a couple of points about the equilibrium force system and compatible displacement system below.
2.2 The equilibrium force system
As the name suggests, the equilibrium force system is just a system of forces in equilibrium. In the context of a truss structure, the equilibrium force system is made up of the externally applied forces and the internal axial forces in the members.
Since the system of forces is in equilibrium, there is no resultant force. This means that there is no net work done by the force system as it moves through the compatible displacement system.
Another way of thinking about this is that the work done by the internal member forces is equal to the work done by the externally applied forces. This is often abbreviated to,
This statement will be the basis of our analysis procedure.
2.3 The compatible displacement system
The compatible displacement system is just a valid displaced configuration for the structure. For the displacements to be a valid compatible displacement system, they must satisfy two conditions:
-
The displacements must be small by comparison to the scale of the structure. This is so that we can make the assumption that the direction of all forces in the equilibrium force system remain unchanged by the deflection. Otherwise we enter the world of geometric non-linearity and our virtual work analysis will be break down.
-
The displacements must be geometrically compatible. In other words they must be a possible set of displacements that do not fundamentally alter or break the structure.
For example, an invalid set of displacements is shown in Fig 2. below. Clearly this will not work, since we’ve imposed a set of displacements that is not compatible with the original structure.
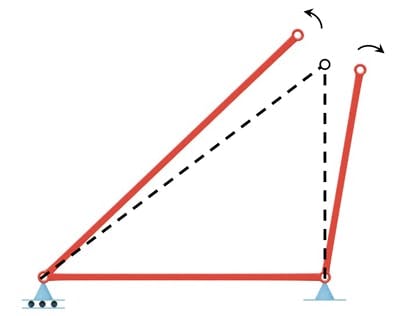
Fig 2. Example of an incompatible (invalid) displacement system.
3.0 The Virtual Work Method Applied to Trusses
Next we’ll set out the analysis procedure itself. As we said above, the virtual work method is based on the following statement,
Building on what we learned about strain energy at the start of our discussion, we can restate this mathematically as,
where represents an externally applied force, is a displacement along the line of action of , is an internal axial force and is a corresponding member extension. We’re summing across all external forces and all member axial forces in this equation.
If we imagine trying to determine an unknown displacement, the equilibrium force system will be virtual ( virtual force applied) and the unknown real displacement will be the compatible displacement system. So in the previous equation:
- will be an externally applied virtual load, applied at the location and in the direction of the desired displacement.
- will be the real unknown displacement.
- will be the virtual internal member forces induced by the virtual applied externally to the structure
- will be the real member deformations consistent with the overall displacement of the structure (and )
In this case, and are the real compatible displacement system and and are the virtual equilibrium force system. You should be able to see the versatility of this method now in comparison to the strain energy analysis we started out with. If you’re not, you will by the time we complete a numerical example below.
Decoupling the equilibrium force system and compatible displacement system – something facilitated by the principle of virtual work, affords us huge flexibility in how we construct our analysis.
4.0 Truss Analysis Example
Instead of discussing any more theory, let’s just start working our way through an actual example question. Consider the pin-jointed truss structure below subject to a single point load applied vertically at G.
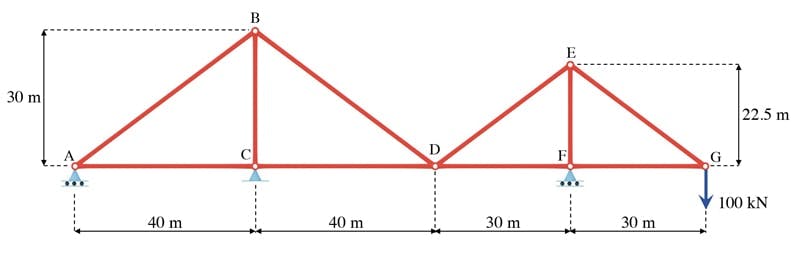
Fig 3. Truss example question.
Our task is to use the virtual work method to determine:
- The reaction force at F.
- The vertical deflection at D.
Calculating the reaction at F using virtual work is really just for demonstration purposes. This is more readily done using simple statics. However, calculating the vertical deflection at D is where the virtual work method really comes into its own.
We can assume a Young’s modulus of and cross-sectional area of for all members.
This question is taken from my Fundamentals of Virtual Work course. So you can continue reading through the solution or watch me work through the solution in the video lecture below.
4.1 Finding the unknown reaction force at F
As it’s a force we’re trying to find, we know that the equilibrium force system will be real, and the compatible displacement system will be virtual. So, we need to apply a virtual displacement, , at F in the direction of the unknown reaction force. This will result in a rigid body rotation of DEGF, Fig 4.
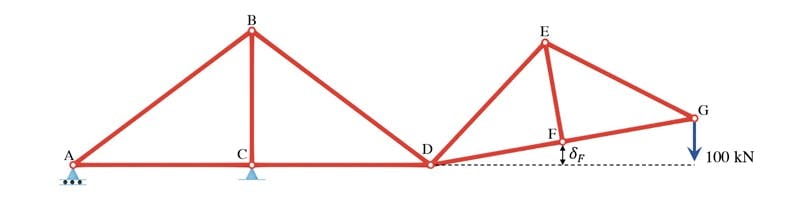
As a result of the rigid body rotation, the unknown reaction force, moves vertically through a distance while the force at G moves vertically through a distance . Remember, we’re assuming all displacements are small by comparison to the scale of the structure so we can neglect any lateral displacement of F and G as the structure rotates about D.
Restating our virtual work equation,
and evaluating the virtual work done by the external forces,
Note the negative sign above is due to the fact that the force is pointing in the opposite direction to the displacement, therefore the work done by the force is negative.
The internal work done which is equal to the internal change in strain energy is zero because the structure is undergoing a rigid body rotation about point D and is not experiencing any strain, therefore,
It’s again worth emphasising that we didn’t need to employ virtual work to determine this reaction. It would have been just as easy to break the structure at D and consider equilibrium of the sub-structure DEGF.
4.2 Finding the unknown displacement at D
Of more interest is how we use the virtual work method to calculate the vertical displacement at point D. This time, since the displacement is unknown, the compatible displacement system will consist of the actual structural displacement experienced by the structure. The equilibrium force system will be virtual and consist of the virtual force and the corresponding internal forces induced.
Starting again with the virtual work equation,
we recognise that each term is the extension due to the actual loads applied to the structure,
where is the axial force in the element due to the real loads applied to the structure ( at G). This is distinct from which we will define as the internal virtual member force induced by the virtual unit load applied at D. Letting and equal to the term defined above, we can restate the virtual work equation as,
Assuming we’ve applied a virtual load vertically at D, we can further reduce our equation down to,
Now the problems simply boils down to evaluating the and member forces and evaluating the sum on the right hand side of the previous equation.
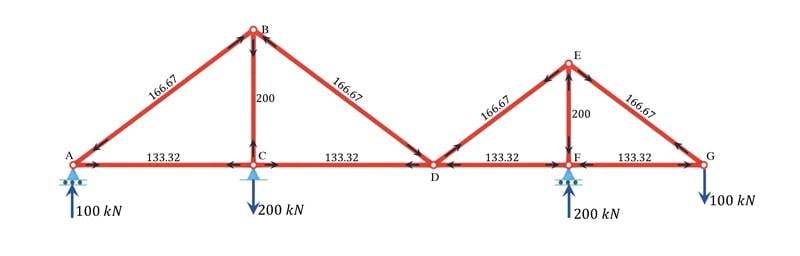
The real forces
The forces are easily obtained using standard truss analysis techniques such as the joint resolution method. The internal member forces are summarised in Fig. 5 below.
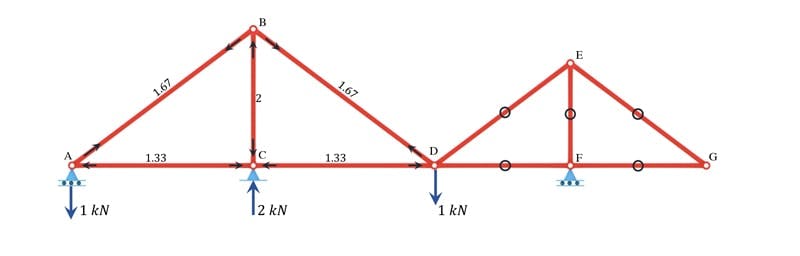
The virtual forces
The forces are obtained using the same approach and are summarised in Fig 6 below. Note that the right side of the structure, to the right of D, consists of all zero-force members, and as such, there is no change in strain energy in this part of the structure.
The only unknown in the virtual work equation at this point is . Evaluating D is made easier by tabulating our data.
| Member | Length | (kN) | (kN) | (kN²m) |
| AB | 50 | -166.67 | 1.67 | -13917 |
| AC | 40 | 133.32 | -1.33 | -7093 |
| BC | 30 | 200 | -2 | -12000 |
| BD | 50 | -166.67 | 1.67 | -13917 |
| CD | 40 | 133.32 | -1.33 | 7093 |
| -54020 |
Adding up the elements in the right hand column we obtain . This can now be divided by the axial rigidity, , to obtain the vertical deflection at D,
The negative sign here indicates that the deflection at D is in the opposite direction to the direction of the virtual load applied, i.e. the deflection is upwards – which makes sense qualitatively for the structure.
5.0 Validating results with the EngineeringSkills Truss Calculator
In this section we’ll compare the results obtained above using the virtual work method with the output from the EngineeringSkills free truss calculator. This will confirm what we’ve seen above, using a different analysis method (the calculator is based upon the direct stiffness method).
More importantly, if you use the calculator, you’ll have a way of testing solutions to practice questions you come up with yourself. We’ve seen above how to apply the theory to one question, but to really get comfortable using the virtual work method will take practice. So, let’s work through validating our results above so that you can do the same on whatever practice questions you come up with.
You can watch me walk through the process in the video below or continue reading step by step.
5.1 Defining the structure and loading
We need to define each node with a number, an x-coordinate and a y-coordinate. This is best done in a spreadsheet first. You can copy the spreadsheet data template demonstrated here. You can then copy and paste the data directly into the relevant data entry box. I’ve numbered the nodes from 1 to 7, following the same sequence as the original alphabetic annotation.
| Node number | x-coord (m) | y-coord (m) |
| 1 | 0 | 0 |
| 2 | 40 | 30 |
| 3 | 40 | 0 |
| 4 | 80 | 0 |
| 5 | 110 | 22.5 |
| 6 | 110 | 0 |
| 7 | 140 | 0 |
Next, we can define the members by first giving each a unique number and then specifying the node number and each end of the member. Young’s modulus and cross-sectional area can now also be defined for each member. You can input any value for yield stress and self-weight – these won’t be used in the calculation.
| Member number | Node I | Node J | Young’s Modulus (N/m²) | Area (m²) | Yield Stress (N/m²) | Self-weight (N/m³) |
| 1 | 1 | 2 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 2 | 2 | 3 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 3 | 2 | 4 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 4 | 1 | 3 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 5 | 3 | 4 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 6 | 4 | 5 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 7 | 5 | 6 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 8 | 5 | 7 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 9 | 4 | 6 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
| 10 | 6 | 7 | 2.00E+11 | 0.0025 | 2.75E+08 | 78000 |
Now we define the support conditions by stating the node number and true or false to indicate the restraint applied in the x (horizontal) and y (vertical) direction.
| Node number | x-restraint | y-restraint |
| 1 | FALSE | TRUE |
| 3 | TRUE | TRUE |
| 6 | FALSE | TRUE |
Finally, we need to specify the loading by stating the node number and the x-component and y-component of the force applied to that node.
| Node number | Fx (N) | Fy (N) |
| 7 | 0 | -100000 |
After the data has been copied from a spreadsheet into the relevant data entry fields, it should look something like Fig 7.

Fig 7. Completed data entry fields.
The structure will now also be visible in the 3D viewport, Fig. 8. The scale of the individual elements can be adjusted using the scale slider in the control panel on the right.
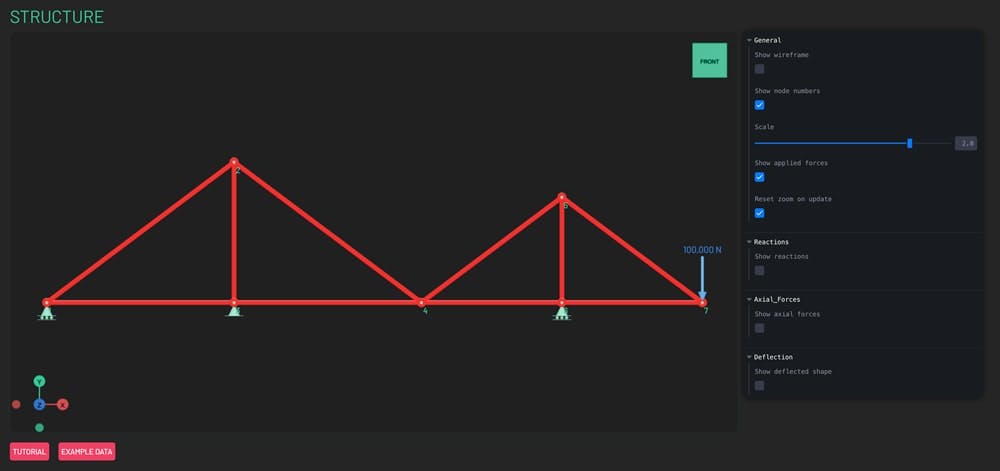
Fig 8. Structure to analyse.
After the structure has been analysed, we can investigate the results directly in the 3D viewport, Fig. 9. We can confirm the support reaction at F (node 6) is indeed . The deflected shape (green line diagram) also shows an upward deflection at D (node 4).
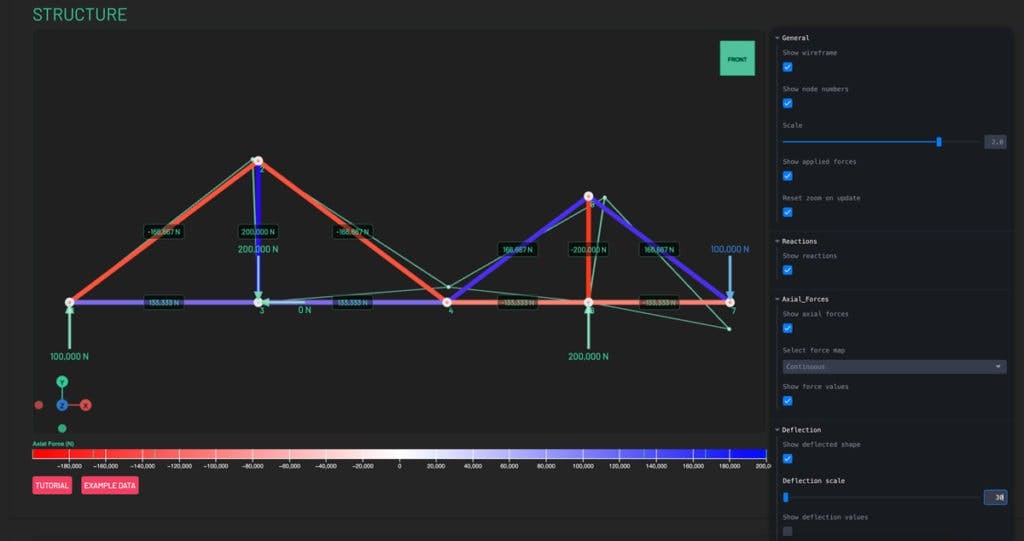
Fig 9. Graphical results.
We can confirm the actual value of deflection by checking the tabulated data further down the page. We can see that at node 4 the vertical deflection is indicated as which is what we calculated using the virtual work method.
Interestingly, we note that there is also a lateral deflection of node 4 of . This is only a tenth of the of the vertical deflection so one could argue that it’s not significant by comparison to the vertical deflection. Clearly the virtual work method was not capable of determining this component of displacement.
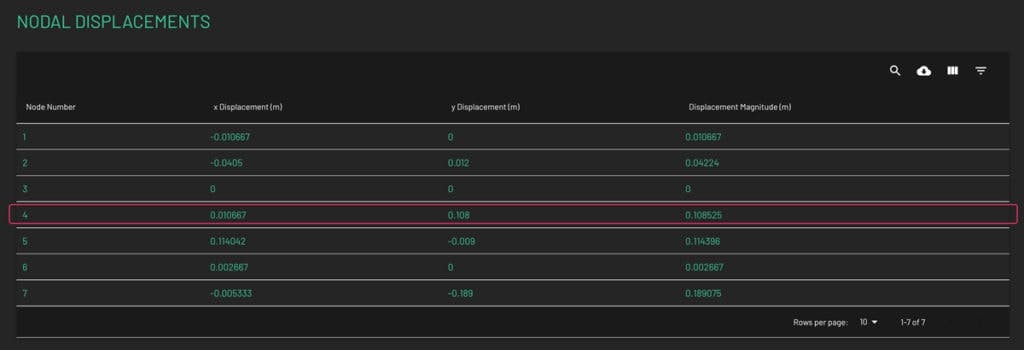
Fig 10. Nodal displacement table.
Now that you’ve seen how to implement the virtual work method and also how to validate or check your worked solutions, you should start coming up with your own test questions to help you embed the technique and get comfortable using it.
That’s all for this tutorial, I hope you found it helpful. Please share this with anyone you think may also find it helpful.
If you want to learn more about virtual work and how to apply it to structural analysis, consider becoming an All Access Member. This will give you access to all EngineeringSkills courses including my three courses focusing on virtual work:
- Fundamentals of Virtual Work
- Mastering Virtual Work
- Analysing Hybrid Indeterminate Civil Engineering Structures
See you in the next one!
Dr Seán Carroll's latest courses.

Featured Tutorials and Guides
If you found this tutorial helpful, you might enjoy some of these other tutorials.
Beam Design using the American Institute of Steel Construction (AISC) Manual
A US-centric deep dive into the design of code-compliant steel beams

Dan Ki