Truss Analysis using the Method of Joints and Method of Sections
![[object Object]](/_next/image?url=%2Fimages%2Fauthors%2Fsean_carroll.png&w=256&q=75)
In this tutorial we’re going to focus on trusses, also known as pin-jointed structures. We’ll discuss their strengths and the common methods of manual truss analysis. We’re going to start at the very beginning by briefly considering what exactly a truss is – but we’ll quickly move on to truss analysis. The wider context here is that before a truss can be designed and member sizes specified, a full truss analysis is required so that we can determine the forces that develop in each member.
If you’re just starting to learn about truss analysis, it will be helpful to have a way of checking the results of your manual analysis. Check out our free truss analysis toolbox below. It’s really important to understand the techniques we discuss in this post – but having a ‘truss calculator’ on hand will be a huge help along the way.
Try our free truss analysis toolbox for calculating reactions, axial forces and deflections. A handy tools for students and professional engineers.
Trusses are one of the first types of structure those new to engineering will tackle. There is a couple of reasons for this; firstly, the truss is a very simple structure, relatively easy to understand and analyse. By deploying some simple mechanics our truss analysis allows us to trace the load path through a truss and visualise how forces are being transmitted through the structure and back to its supports.

Example of a truss railway bridge.
The other reason we focus on trusses early in the study of engineering is because they are so ubiquitous. We see them all around the built environment. They’re simple yet incredibly efficient structures that can span very large distances with relatively little material. It’s this efficiency that makes them well suited as roof and bridge structures. After reading this tutorial, if you want to work through more examples, you can take my course on the Fundamentals of Structural Analysis.
Fundamentals of Structural Analysis
Get to grips with civil engineering structural analysis once and for all.
After completing this course...
- You will understand key concepts such as the moment of a force, static equilibrium and determinacy.
- You will be able to determine the support reactions for structures subject to a range of loading conditions.
- You will learn to use the Joint Resolution Method and Method of Sections to analyse pin-jointed truss structures.
1.0 What is a truss?
Let’s start by nailing down what a truss is. A truss is a structure that consists of a collection of elements connected at pin joints or nodes. In theory, the pin joints provide no rotational resistance and behave as hinges. The benefit of a truss is that the members are predominantly axially loaded. This means they are either in compression, tension or have no force, so-called zero force members. This makes trusses a particularly efficient structural form.
The structural efficiency of trusses is evidenced by the fact that we see truss structures routinely employed to span large distances and efficiently withstand high loads. In this tutorial, we’ll consider 2-dimensional truss structures, but everything we discuss is equally applicable to 3-dimensional trusses, sometimes referred to as space frames. The common tower crane is a good example of a 3-dimensional truss structure.

The tower crane is a great example of a truss structure used to efficiently transmit large loads. The individual structural members in the crane could be reasonably modelled as axially loaded truss elements.
1.1 Theoretical truss behaviour and load paths
As we’ve said, theoretically at least, all truss nodes are effectively pins or hinges. This means that the members meeting at a node are free to rotate relative to each other. As such, moments cannot be transmitted from one member into adjacent members. Only forces can be transmitted through nodes.
⚠️ I’ve covered the differences between theoretical and actual truss behaviour in this post. To fully understand the assumptions inherent in our truss analysis techniques discussed below, make sure to read this post.
From an engineering perspective, a truss, like any structure has one purpose, to transmit externally applied forces through the structure and back into the supports or foundations of that structure. Take the simplest form of truss as an example.
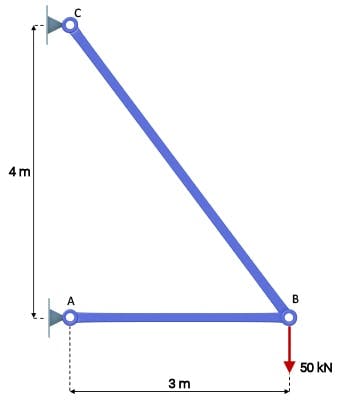
Simple 2-bar truss subject to a single externally applied force
The force applied at node B, must be transmitted through the structure back into the pin supports at A and C respectively. We can think of the external loads travelling along a load path. The engineer’s job is to evaluate the load path and make sure the structural elements along that path can withstand the stresses induced by the loads being transmitted.
Using the three equations of statics , and , the reactions at A and C are easily evaluated;
Confirm these values yourself through calculation. In order for these reactions to develop at the supports, member AB must transmit a compression force of while member BC transmits a tension force of . We can see this indicated on the right hand load path diagram below. By the end of this tutorial, you will be comfortable determining these load paths for statically determinate truss structures.

Simple 2-bar truss subject to a single externally applied force (left) and resulting load path (right).
2.0 Joint Resolution Method of Truss Analysis
Now that we’ve clarified what a truss is and the concept of a load path describing the transmission of forces through the structure, the next task is to work out how to identify the forces along the load path. In other words we want to be able to work out the forces developed in each of the members in response to external loading.
We’ll focus on two similar techniques that make use of the equations of static equilibrium. They are:
- the joint resolution method
- the method of sections
In both cases, we must first determine the support reactions for the structure. Only then can we employ the joint resolution method, method of sections or a combination of both.
We’ll start by considering the joint resolution method which involves evaluating force equilibrium at each joint or node and using the equations of statics to solve for the unknown member forces. Consider the two bar truss again, shown below as a free body diagram.
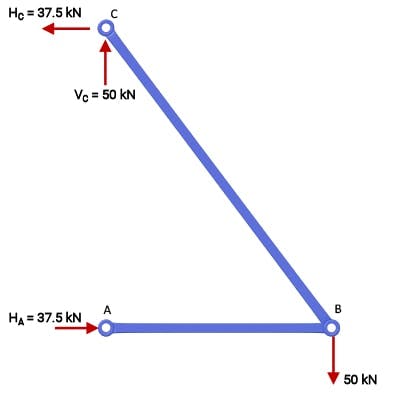
Free body diagram of a 2-bar truss
The joint resolution method requires us to evaluate the sum of the forces meeting at a joint. These forces can be resolved into two orthogonal (mutually perpendicular) directions allowing us to evaluate two equations of force equilibrium. Thus we have two equations from which we can determine two unknowns. So, using the method of joints we can only start at a joint that has a maximum of two unknown member forces. For this simple structure, we can consider any of the three nodes, we’ll start with node B.
We isolate the joint by cutting the members meeting at that joint. Making these cuts we reveal the internal member forces, for now labelled as and where the indicates we are assuming (until proven otherwise) that the forces are tension forces.
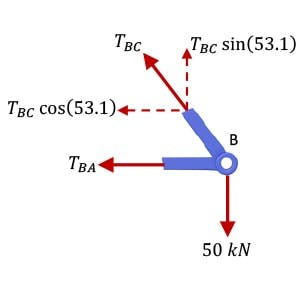
Free body diagram of joint B
A free body diagram of the joint is then evaluated by taking the sum of the forces in the horizontal and vertical direction and equating them to zero to reveal the unknown member forces (remember two unknowns, so two equations required). In the following analysis, note that basic geometry gives us the angle . Now consider force equilibrium of joint B:
Notice here that evaluates to a positive number and therefore our assumption that the force in member BC is a tension force is correct. Now evaluating horizontal force equilibrium,
Here the negative value tells us that the force in member BA is actually opposite to our initial assumption and therefore a compression force. This completes the analysis of this simple truss. It is worth reflecting on the direction of the arrows indicating tension and compression below.
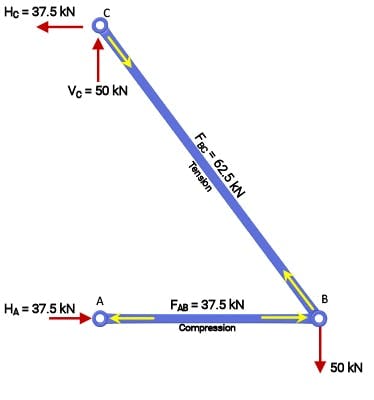
Free body diagram of joint A showing internal member forces (the load path).
For member AB in compression, the yellow force arrows point outward, as if to resist a force compressing the member. By the same analogy, the force arrows for member BC point inwards as if to resist a force trying to pull apart or stretch the bar. This can initially be counter-intuitive so make sure you’re happy with this convention before proceeding, otherwise you’ll get terribly confused later on.
That’s the joint resolution method in a nutshell. We’ve only demonstrated it so far for a very simple truss but the process is exactly the same no matter how big your truss gets. As long as you can identify a node within your truss structure that has no more than two unknown member forces passing through the node, you can deploy the joint resolution method. We’ll see this in action again a little later!
3.0 Method of Sections Truss Analysis
Now we can consider the other tool at our disposal, the method of sections. Instead of isolating a single joint, the method of sections involves us making an imaginary cut through the entire structure. In doing so, we reveal the internal member forces in the members our plane cuts through. We can then evaluate equilibrium of either of the two sub-structures created by the cut.
This method of structural analysis brings into play a third equilibrium equation; because all of the forces acting on the sub-structure no longer all pass through the same point, we can now consider the sum of the moments about any point which, is our third equation.
Since the structure is in a state of static equilibrium, the sum of the moments (just like the forces) must equal zero. So we now have three equations of statics at our disposal. The key thing to remember with the method of sections is that our plane cannot cut through more than three members with unknown member forces.
As usual, the best way to understand this technique is by working through an example. So consider the simple Warren truss below subject to point loads at nodes B and D.
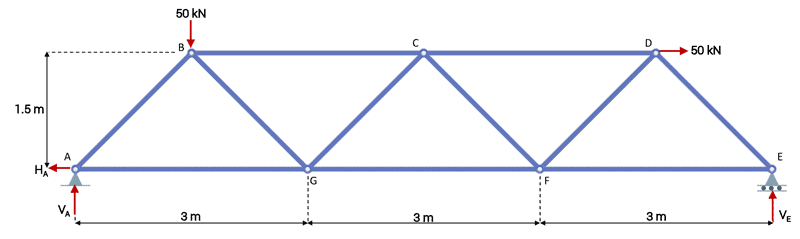
Warren truss subject to two point loads
Reactions
As with any statically determinate analysis, the first task is to determine the support reactions. We’ll start by considering the sum of the moments about point A which must equal zero. We’ll assume clockwise moments are positive.
Next we can evaluate the sum of the forces in the vertical or direction to determine the remaining unknown vertical reaction. Assuming upward pointing forces are positive, we have,
Finally, by inspection we can say that the horizontal reaction is,
Section 1
To demonstrate the method of sections, let’s start by considering a vertical section cutting the structure between nodes G and C. This will cut through members BC, CG and GF which will reveal the internal forces in those members. As we do for the method of joints, we’ll assume these forces are tension forces and therefore the force arrows point away or out of the cut member.
The sub-structure to the left of the cut (pictured below) must now be in a state of static equilibrium under the influence of the externally applied forces, reactions at A and internal member forces, , and . So, we have three unknowns and three equations, we’re now able to solve for the member forces.
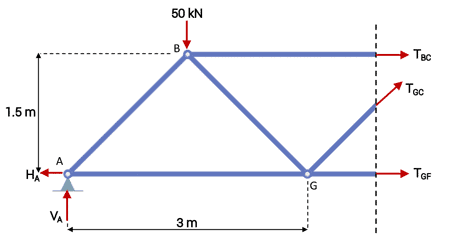
Warren truss with vertical cut revealing three unknown member forces
We’ll start by using the moment equation and evaluating the sum of the moments about point G. Point G is a good starting point because two of our unknowns pass through it and so will disappear from the moment equation, leaving only that we can directly solve for.
Now the fact that evaluated to a negative number means that the force arrow actually points in the opposite direction, meaning that is a compression force,
Next, if we evaluate the sum of the forces in the vertical direction we can solve for ,
And finally we can determine the remaining unknown by considering horizontal force equilibrium and assuming forces to the right are positive,
The method of sections is a helpful technique, because we can make a cut anywhere within the structure to determine the member forces. We don’t need to know any of the other internal member forces. So for example, we didn’t need to know what the forces were in members AB, AG or BG before we made our cut.
If we were only using the joint resolution method, we would have to work our way from the support nodes towards the area of interest and evaluate the forces at each node along the way, which could become tedious for a larger structure.
Let’s try another cut, this time with a cutting plane between D and F and considering the sub-structure to the right of the cutting plane.
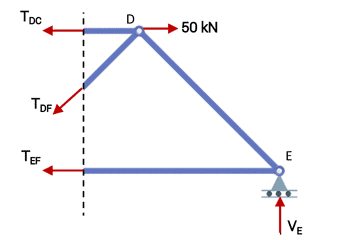
Warren truss with vertical cut revealing three unknown member forces
Again note that our cutting plane has cut through no more that three members with unknown internal member forces. This is key, if our cut reveals any more that three unknowns, we won’t have enough equations to solve for them all. A sensible starting point this time is to consider the sum of the moments about point D, eliminating two unknowns from the moment equation.
Evaluating vertical force equilibrium next,
And finally, horizontal force equilibrium,
Now is a good time to summarise where we are in the analysis,
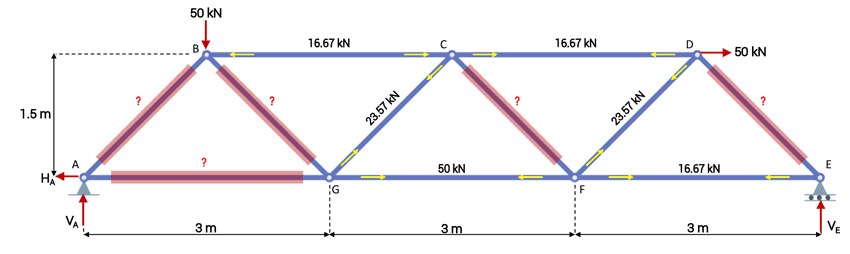
Summary of internal members forces so far with remaining unknown forces highlighted in red
We could continue to use the method of sections and make more cuts in the structure or we could use the method of joints to finish out our analysis. For the sake of variety, we’ll use the method of joints from here on.
Joint A
Starting with joint A we cut the members meeting at the joint to reveal their unknown internal forces,
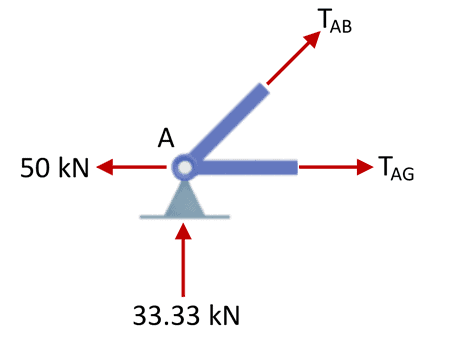
Truss joint A
Remember from our discussion above, we only have 2 equations to work with now and so we can only evaluate joints with a maximum of two unknown member forces. Evaluating vertical force equilibrium first,
Now considering horizontal force equilibrium,
Joint B
Moving on to joint B,
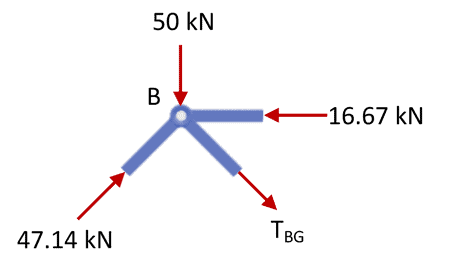
Truss joint B
We only need to evaluate vertical force equilibrium to determine our only unknown here, .
Joint C
Considering horizontal force equilibrium of joint C next.
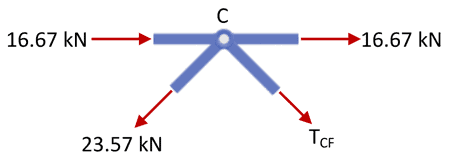
Truss joint C
Joint E
And finally, vertical force equilibrium of joint E.
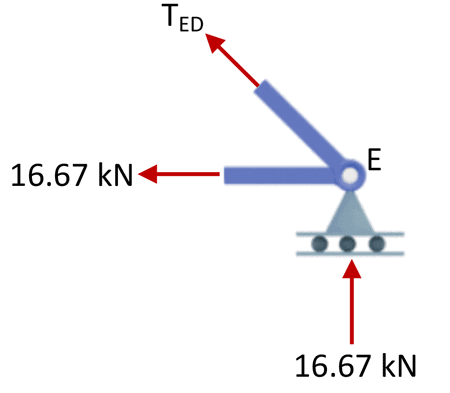
Truss joint E
Now that we’ve evaluated all of the internal member forces, we can summarise them below.
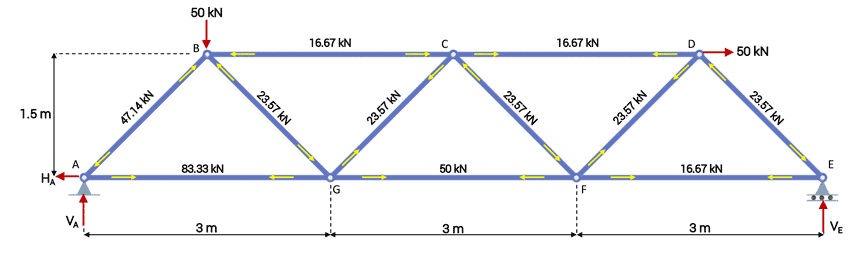
Summary of all internal member forces representing the complete load path for the structure under these external loads.
Hopefully these few examples have given you a clear idea of exactly how to go about analysing a statically determinate truss. The high level steps are the same each time; first identify your support reactions, then start working your way through the structure using the joint resolution method, method of sections or both.
Remember, when using the joint resolution method you have two equations to work with so analyse joints that have up to two members with unknown forces coming into the joint. When using the method of sections, you unlock a third equation to work with, the moment equation. So now, whatever section you take through the structure, it cannot cut through more that three members with unknown internal forces.
When trying to perform a truss analysis, you may find that you can’t start the analysis or part-way through you can’t advance any further. There may be no suitable cuts to make or joints to analyse. In this case you’re likely dealing with a statically indeterminate truss and the methods discussed here won’t work.
I’ve written a little more on the concept of truss indeterminacy in this post and I’ve written up a full tutorial on an alternative solution method that is applicable to indeterminate trusses in this post. So check those out for more information.
That’s it for truss analysis in this post, see you in the next one.
Dr Seán Carroll's latest courses.

Featured Tutorials and Guides
If you found this tutorial helpful, you might enjoy some of these other tutorials.
Building a Parametric Frame Analysis Pipeline with OpenSeesPy and OpsVis
We’ll build a script to perform 2D elastic frame analysis and use OpsVis for fast visualisation of model behaviour

Dr Seán Carroll
Column Buckling - Realistic Buckling Behaviour
Real-world columns rarely exhibit the strict mathematical buckling behaviour predicted for perfectly loaded, perfectly straight columns

Dr Seán Carroll
Building a Beam Deflection Calculator in Python
Build a beam deflection calculator in Python by numerically integrating the bending moment diagram

Dr Seán Carroll