
Non-linear Finite Element Analysis of 2D Catenary & Cable Structures using Python
Build an iterative solution toolbox to analyse structures that exhibit geometric non-linearity due to large deflections.
- You will understand the concept of geometric non-linearity and when it should be considered.
- You will learn how to modify the element stiffness matrix to account for large deflections and changes in geometry.
- You will implement a Newton-Raphson solution algorithm that seeks to converge on the final state of the structure.
- You will build a workflow that uses open-source modelling tools to quickly generate structural geometry.
After completing this course, you’ll have built an iterative numerical solver for cable and truss structures that exhibit geometric nonlinearity due to large deformations.
This course focuses on building the understanding and tools to analyse structures that undergo large deflections when loaded. Large changes to the geometry of a structure can alter the internal stress distribution. This is known as geometric non-linearity and requires a more sophisticated solution strategy.
We’ll place particular emphasis on cable and catenary structures as these are classic examples of structures whose deformation under load can lead to geometric non-linearity. However, the code developed can be equally deployed to flexible truss structures.
The tools developed in this course are not meant as a replacement for commercial non-linear solvers (we’re not going to be rebuilding SAP2000! 🙂) – the objective here is to build your understanding of the behaviour and the best way to do this is by implementing what you learn by building your own solver.

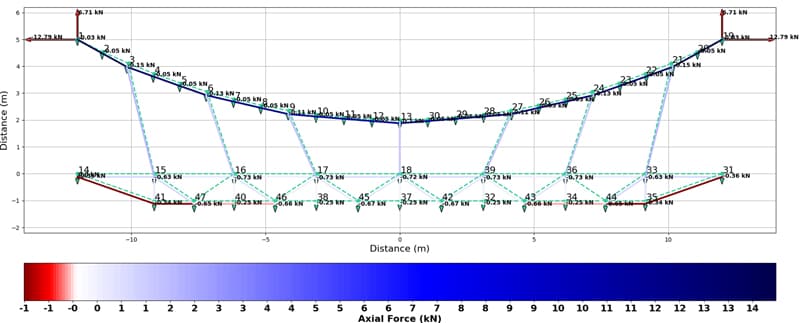
Your final code will be capable of handling structures like the one above that consist of a mixture of axially loaded cable (tension only) and bar (tension and compression) elements. Our solver implements an iterative algorithm, so a solution that converges is not always guaranteed! We’ll be leaving the relative comfort and certainty of linear analysis behind – welcome to geometric non-linearity!
Course prerequisites
Much of what we cover in this course is about how to implement an iterative solver for the tricky problem of geometric non-linearity. This essentially involves implementing and updating the direct stiffness method in a loop. So, you should have a good understanding of the direct stiffness method for axially loaded elements.
Even if you have a theoretical understanding of the direct stiffness method, I still recommend that you complete my course on applying the direct stiffness method to truss structures.
That course is called, The Direct Stiffness Method for Truss Analysis with Python and it’s my entry point into matrix-based structural analysis.
A lot of the code we write in this course, for example how to build the overall structure stiffness matrix and basically all of the nuts and bolts of the basic stiffness method, is written and explained in more detail in that course. You’ll lower the cognitive load on yourself if you encounter this code in a less demanding context first.
The next question to address is how much Python do you need to know? Technically none, however, because there is a lot to contend with in this course, I would say trying to learn Python on top is going to be quite demanding. It’s not that the coding we’ll do is any more complex than what we’ve done in previous courses, it’s just about managing the cognitive demand.
This is another great reason to take the prerequisite course. Get familiar with Python and how I implement the direct stiffness method in that introductory course first. This will leave you in a great position to tackle this course and really focus on what’s new and challenging about analysing non-linear structures.
We’ll develop our Python code using the versatile Jupyter development environment. When you complete this course you’ll have a range of standalone code notebooks to deploy on your own projects. The code developed within each section of the course is also provided for download as a reference.
Course Breakdown
Section 1: Introduction and Course Breakdowns
In this short introductory section, we’ll take a tour of the course, section by section, to give you an idea of what to expect as you move through the course. We’ll also briefly discuss the course prerequisites.
Section 2: ‘Heavy’ cables – the linear solution
In section 2 we’ll start our analysis of cable behaviour. Cables very often undergo changes in their geometry under loading, either due to cable extension, directly applied loads or flex in the cable supports – they are the classic example of a non-linear structure. In this section, we’re going to establish a linear (closed-form) cable solution that ignores non-linear effects. This will provide a baseline case to test our non-linear code against later.
Section 3: Getting Comfortable with Non-linearity
In section 3, we’ll start to talk about non-linear structural behaviour, before focusing on geometric non-linearity in particular. The aim of this section is to take any mystery out of the term ‘geometric non-linearity’. We’ll also explore, at concept level, how we might set about solving for the behaviour of a non-linear structure. We’ll introduce the Newton Raphson method which informs the main architecture of the solver code we’ll write later on.
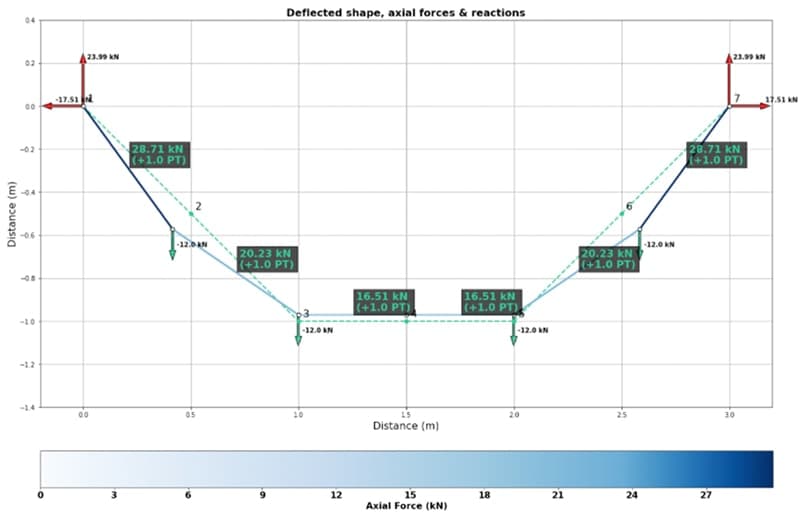
Section 4: The Non-linear Stiffness Matrix
One of the central elements of a matrix-based non-linear structural analysis is a stiffness matrix that can capture the influence of large deflections of the structure. In section 4 we’ll focus on deriving a form of non-linear element stiffness matrix that can do just that. Familiarity with the material in the prerequisite course will be helpful here.
Section 5: Building our 2D Solver Toolbox
Now that we have a stiffness matrix that can reflect progressive stiffening or softening due to large deformations and we understand, conceptually at least, how to iterate towards a solution, it’s time to build out the code that can bring these ideas to life. In section 5, we’ll do the bulk of our code development. In bitesize chunks, we’ll build our solver, bit-by-bit. By the end of this section, you’ll have a functioning non-linear solver.
Section 6: Visualising the Results
After building a solver, next, we need to turn our attention to visualising the output results. This is the focus of section 6. We’ll build out the data visualisation that brings our solution to life and allows us to explore how the structure evolves towards its final equilibrium state.
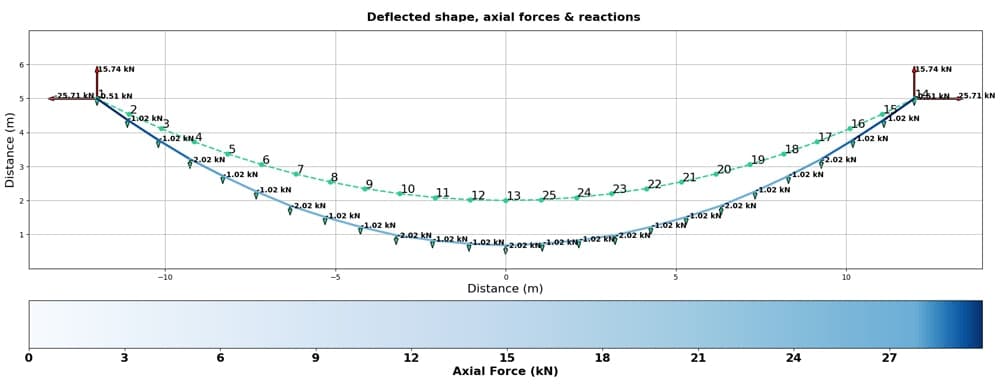
Section 7: ‘Heavy’ Cables – the Non-linear Solution
In section 7 we’ll return to a conversation we started at the very beginning of the course. We’ll use our new solver to simulate the cable we kicked the course off with. We’ll compare our code’s results with our earlier linear solution. We’ll be able to closely approximate the linear solution but also observe the emergence of non-linear behaviour as the axial stiffness of our cable is progressively reduced.
Section 8: Modelling Initial Geometry in Blender
In section 8 we’ll take a break from pure coding and detour over to Blender, the free 3D modelling tool we’ll be using to generate structural geometry. If you’ve taken some of my other structural analysis courses you’ll be familiar with how we use Blender. If you’re completely new to Blender, I’ve included an appendix section at the end of the course to help you get set up and familiar with Blender.
Section 9: Mixing Cables and Bars in the Same Model
In the final section of the course, we’ll expand our code to handle structures that consist of both bar and cable elements. One of the features of a cable is its inability to resist compression. Our code doesn’t yet capture this behaviour – we’ll address that in this final section of the course. We’ll also complete the modelling and analysis of a cable-stayed lattice tower – a classic example of a conventional and commonly found structure that utilises geometrically non-linear cables.

Who this course is for
- Students and professional engineers who are familiar with methods of linear structural analysis and want to learn about non-linear behaviour.
- Anyone who has taken my linear 2D truss analysis course and wants to extend their analysis capabilities beyond linear structures.
- Students and professional engineers who want to learn more about how to implement iterative methods of analysis in Python.
The codes developed in this course are for educational purposes only and are not tested or certified for use beyond the educational scope of this course. Always employ your own engineering judgement first and foremost, regardless of what the computer says!

Download your personalised Certificate of Completion once you’ve finished all course lectures.
Applying for jobs? Use your Certificate of Completion to show prospective employers what you’ve been doing to improve your capabilities.
Independently completing an online course is an achievement. Let people know about it by posting your Certificate of Completion on your Linkedin profile or workplace CPD portfolio.

